5. Le son¶
Un son est une histoire d’énergie et de vibrations. Un son émerge quand des molécules subissent une pression initiale, ce qui va les amener à avancer et entrainer ce mouvement sur les molécules devant immédiatement voisines en leur transmettant une grande partie de cette énergie. Suite à ce nouveau mouvement, elles repartent en arrière pour retrouver leur position d’équilibre ayant transmis cette énergie initiale aux molécules voisines qui à leur tour vont se comporter de la même manière.
Toutes ces «tranches» de molécules vont donc osciller successivement, formant une onde qui va se déplacer au sein du milieu matériel : air, eau, caoutchouc par exemple. C’est ce que l’on peut observer lorsqu’un projectile heurte une flaque d’eau : à partir du point d’impact, se forme progressivement une onde circulaire qui s’étend et se propage à la surface de l’eau.
Le son est donc une vibration mécanique, nécessitant un milieu matériel : s’agissant des sons que nous entendons tous les jours, le milieu matériel est bien évidemment l’air ambiant.
On appelle fréquence du son, la vitesse avec laquelle ces molécules vibrent. Plus la vibration des molécules est rapide, plus le son est aigu : on parle de fréquence élevée. Inversement, plus la vibration est lente, plus basse est la fréquence. Une corde de guitare détendue vibre moins vite que sa voisine très tendue, elle va produire un son plus grave avec une oscillation bien plus lente.
Le niveau sonore correspond lui à la hauteur de l’oscillation : on parle d’amplitude.
Ce phénomène physique d’oscillation des molécules dans l’air est capté par notre oreille en mettant en vibration nos organes qui vont convertir cette pression reçue en signaux électriques transmis au cerveau. Votre musique préférée est donc une addition de sons avec des fréquences et amplitudes différentes qui vont vous fait vibrer au sens propre… comme au figuré !
Entre phénomène physique et organe sensoriel, le son physique (on parle également de son analogique) va être un ensemble d’oscillations, de vibrations, définies par des fréquences et des amplitudes.
Chaque «son élémentaire» peut ainsi être assimilé à une courbe comme celle décrite dans la vidéo : on parle de courbe sinusoïdale, ou encore de sinusoïde. Les sons ou la musique que vous écoutez n’est autre qu’une somme de ces courbes «convenablement» arrangées.
La question est de savoir comment ramener ces oscillations sinusoïdales combinées ensemble en un ensemble de 0 et 1 pour être stockées numériquement dans un ordinateur, comme les nombres, images et les caractères.
Le saviez-vous ?
Les casques à conduction osseuse transmettent les vibrations directement à l’os temporal du crâne : la cochlée qui est nichée dans cet os va vibrer et transmettre les informations électriques au cerveau, comme le ferait un signal passant par le tympan et le marteau.
Le saviez-vous ?
Vous rappelez-vous l’explosion de l’étoile de la mort dans Star Wars ? Eh bien un son pareil ne peut exister dans l’espace : il n’y a pas assez de molécules à agiter, l’énergie transmise par l’explosion ne peut pas se propager de la sorte.
5.1. Numérisation¶
La conversion d’une grandeur physique analogique continue – température, vitesse du vent, position d’une girouette, etc. – en données numériques digitales est appelée numérisation. Elle est réalisée en trois étapes : un échantillonnage, une quantification puis un encodage.
Le processus de numérisation engendre une quantité d’information (des bits) qui vise à représenter, aussi précisément que nécessaire, la grandeur physique sous une forme manipulable par les ordinateurs.
Il s’agit donc d’un compromis entre la qualité de la représentation et les coûts engendrés par un fichier plus grand, qui prend plus de place de stockage, plus de temps à copier, à transmettre sur un réseau et/ou nécessite une puissance de calcul plus importante pour la numérisation (conversion analogique/digitale) et pour la reconstruction (conversion digitale/analogique).
Ci-après, un signal continu sera numérisé, mettant en évidence le rôle et les effets des différents paramètres de la numérisation. Il s’agira pour l’exemple de l’intensité sonore telle qu’elle peut être capturée par un microphone.
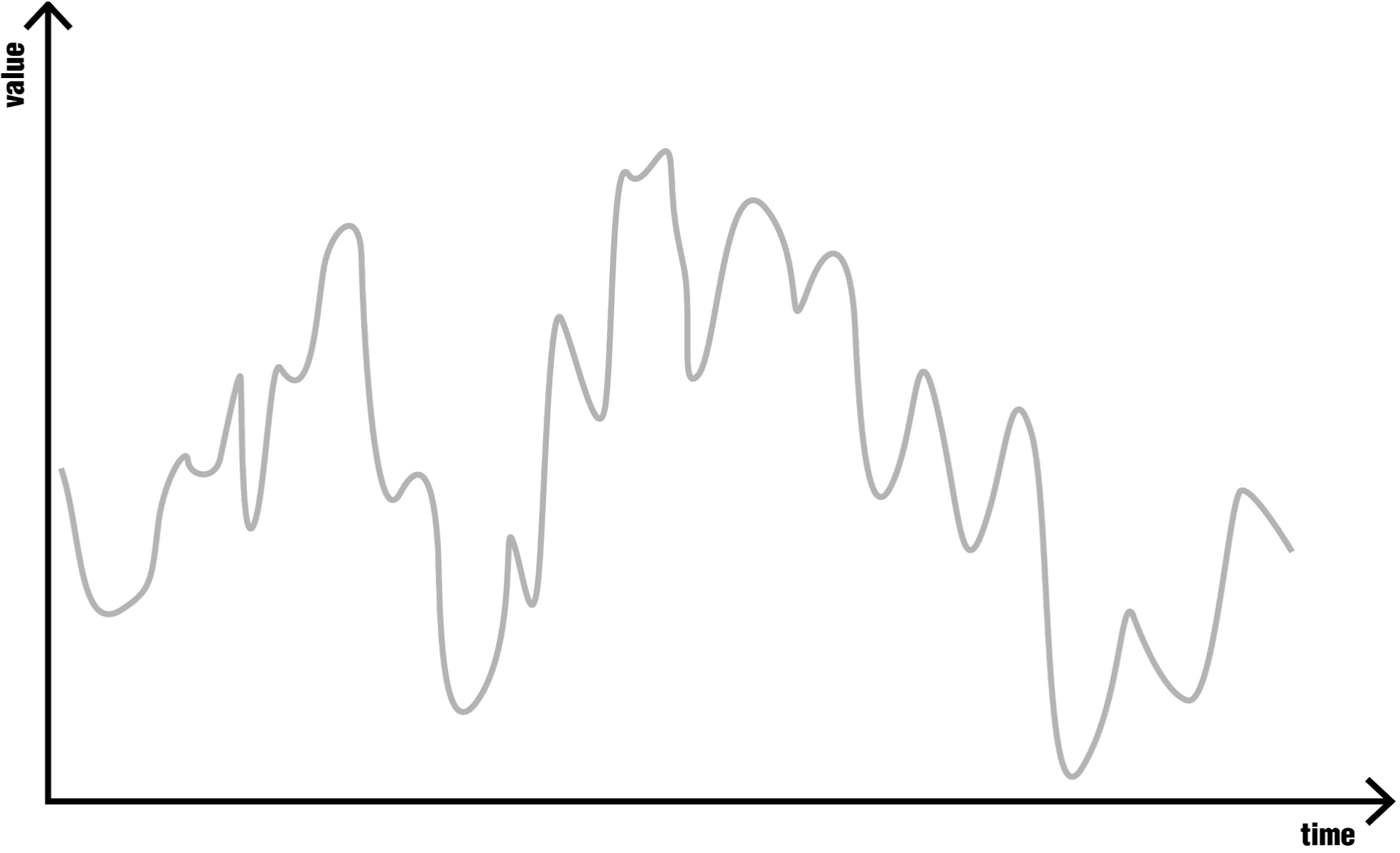
Fig. 5.1 Signal continu à numériser, par exemple un son.¶
Le saviez-vous ?
Les sons, tels que perçus par notre ouïe, résultent de la vibration de l’air, prenant la forme d’oscillations cycliques de la pression. Ces oscillations peuvent être capturées par la membrane d’un microphone et générer un signal électrique qui peut être numérisé.
En échange, un signal électrique qui stimule un haut-parleur produit des oscillations de la pression de l’air qui peuvent à leur tour être perçues. Ce signal peut provenir de la reconstruction d’un signal numérisé.
5.2. Échantillonnage¶
L’intervalle temporel entre deux mesures est appelé la période d’échantillonnage. La fréquence d’échantillonnage (sampling rate) est le nombre de mesures prises par seconde, exprimée en Hz.
Les limites pratiques d’un échantillonnage sont fixées par la fréquence de Nyquist, qui, de façon très simplifiée, indique que l’information découlant d’un processus dont la fréquence est supérieure à la moitié de la fréquence d’échantillonnage sera perdue lors de la numérisation. Il ne sera donc jamais possible d’avoir une représentation complète d’un processus complexe, tout au mieux une représentation suffisante. Comme toute activité d’ingénierie, la solution retenue résulte d’une pesée d’intérêts et non d’une évidence pointant vers une solution unique.
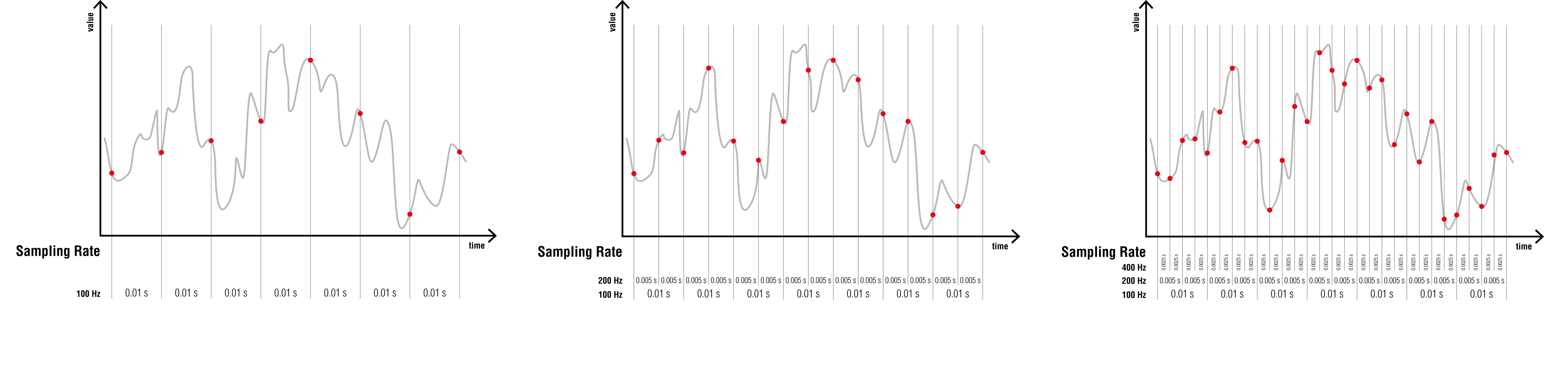
Fig. 5.2 Effet de la fréquence d’échantillonnage (sampling rate : 100, 200 et 400 Hz) sur la représentation obtenue par numérisation.
Plus la fréquence est élevée, plus la quantité d’information collectée est importante. Dans tous les cas, les détails du signal qui se déroulent entre les échantillonnages sont perdus.¶
Sachant que l’oreille humaine ne perçoit globalement que les fréquences comprises entre 20 et 20000 Hz, une fréquence d’échantillonnage supérieure à 40 kHz permettra de restituer l’ensemble de l’information physiologiquement perceptible par l’oreille humaine.
Le saviez-vous ?
La fréquence d’échantillonnage de 44.1 kHz a été retenue dans les années 1970 pour permettre l’utilisation des bandes vidéo pour stocker les enregistrements numériques. Ces bandes représentaient le meilleur rapport volume de stockage/prix pour l’époque.
Cependant, les formats vidéos sont cadencés sur la fréquence du système électrique local : 60 Hz pour le NTSC américain (et 30 images par seconde) ; 50 Hz pour le PAL européen (et 25 images par seconde). En choisissant le multiple commun de 44.1 kHz, la norme permettait d’être utilisée avec les deux formats NTSC et PAL comme support de stockage physique pour le transport du “master” stéréo en vue de son impression sur des CDs.
Depuis, avec la disparition des cassettes vidéo comme supports de données, puis l’apparition du support DAT, l’échantillonnage à 48 kHz s’impose progressivement (avec ses multiples 96 et 192 kHz). Ces valeurs ont l’avantage d’être des multiples de huit, ce qui est toujours favorable dans le domaine informatique.
De plus, ces fréquences simplifient la synchronisation avec les enregistrements vidéo en 24, 25, 30, 60, 100 et même 120 images par seconde. Les multiples de 48 kHz sont donc des fréquences d’échantillonnage de choix pour la diffusion HDTV, notamment.
C’est la raison pour laquelle l’échantillonnage de la musique en qualité “CD” est réalisé à 44.1 kHz, en prenant en compte une petite marge pour l’utilisation de filtres passe-bas lors de l’enregistrement.
Une fréquence d’échantillonnage inférieure génère un son dont la qualité est dégradée, à commencer par la précision des sons les plus aigus, aboutissant à une numérisation qui rappelle le son des anciens téléphones analogiques dont les fréquences transmises étaient limitées à 3.4 kHz pour des raisons techniques.
D’ailleurs, les premiers téléphones mobiles ont par la suite répliqué ce niveau de qualité sonore comme base pour leur échantillonnage numérique (norme G.711). Selon la norme utilisée, les téléphones mobiles actuels transmettent quant à eux les fréquences jusqu’à 7 kHz (normes G.722.2 et suivantes).
Une fréquence d’échantillonnage supérieure génère une plus grande quantité d’information, sans ajouter de valeur qualitative pour la très grande majorité des auditeurs.
Le choix de la fréquence d’échantillonnage résulte donc d’une délicate balance entre coûts (taille des données) et bénéfices (qualité de la numérisation).
5.3. Quantification¶
La quantification d’une valeur échantillonnée requiert de déterminer la précision de chaque échantillon, ce qui détermine le volume de données générées. Cela découle de la représentation des entiers par les ordinateurs.
La précision de l’encodage est donnée par la profondeur de l’échantillonnage (bit depth) exprimée en bits (binary digits). Comme pour l’échantillonnage, plus la profondeur de l’échantillonnage est importante, plus la quantité d’information générée est importante.
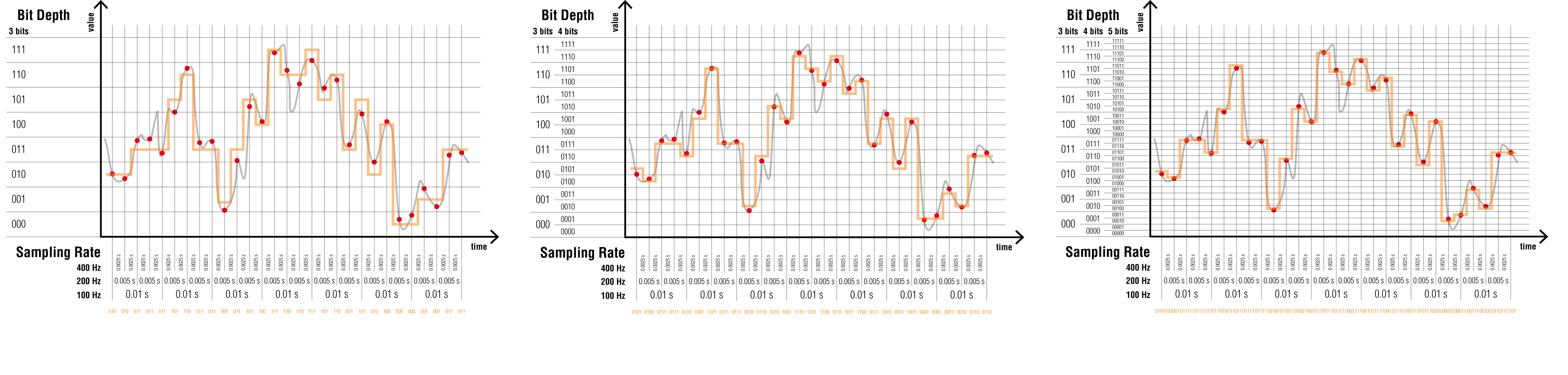
Fig. 5.3 Effet de la profondeur de l’échantillonnage (bit depth : 3, 4 et 5 bits) sur la représentation obtenue par numérisation. Plus la profondeur est importante, plus la discrimination du signal et la différence entre les basses et les hautes intensités est importante. La quantité d’information générée (le nombre de 0 et de 1) devient également plus importante.¶
Lorsque l’ensemble de la plage des valeurs possibles est utilisée pour l’encodage, la profondeur de l’échantillonnage définit la plage dynamique disponible. Elle est définie entre la valeur encodée la plus petite (0, par exemple) et la valeur encodée la plus élevée (\(2^n - 1\) pour une valeur encodée sur n bits, par exemple). Elle correspond également à une idée de précision ou de discrimination des échantillons.
Ici encore, l’oreille humaine ne peut percevoir ni les intensités les plus faibles (inférieures au bruit émis par l’individu lui-même) ni les intensités au-delà du seuil de douleur.
Une précision minimale (environ 8 bits) est ainsi nécessaire pour restituer agréablement un enregistrement respectant les subtilités de l’expression orale (entre voix posée et criée, par exemple).
Au-delà de 16 bits, une profondeur d’échantillonnage supérieure engendre une plage dynamique qui n’a pas d’application pertinente pour la restitution des sons pour la plupart des humains, au coût d’une plus grande quantité d’information collectée.
À l’inverse, il est nécessaire de gérer correctement la plage d’amplitude dans laquelle la numérisation du signal se déroule. Cela s’opère en agissant sur le paramètre de gain du signal.
La distorsion découle d’un signal dont l’amplitude dépasse les capacités d’encodage du système. Dans ces conditions, un ajustement du gain d’entrée est nécessaire pour rester au plus proche des limites du système, sans les franchir.
La numérisation d’un signal dont l’amplitude serait par trop réduite débouche au contraire sur un encodage qui contient moins d’information, ce qui limite les opérations réalisables numériquement par la suite sans détériorer la qualité du signal.

Fig. 5.4 Effet du gain (trop haut, correct, trop bas) sur la représentation obtenue par numérisation. La distorsion résulte de valeurs très différentes de celles du signal original. Cette aberration du processus de numérisation ne peut plus être corrigée, car de l’information a été perdue au passage. À l’inverse, un gain trop faible nuit à la dynamique de l’information collectée, c’est-à-dire que l’écart entre la valeur retenue la plus faible et la plus élevée n’est qu’une fraction de l’intervalle disponible. Il en résulte une perte de précision.¶
On notera finalement que l’échantillonnage et la quantification travaillent ensemble pour définir la qualité du signal numérisé. Ces deux paramètres ne sont pas complètement indépendants. Leur choix est réalisé en fonction du résultat escompté et de ce que l’on cherche à réaliser avec le signal numérisé.
Pour l’intensité sonore par exemple, une fréquence d’échantillonnage insuffisante ne peut pas être compensée par une profondeur d’échantillonnage supérieure. La qualité du résultat n’est pas améliorée.
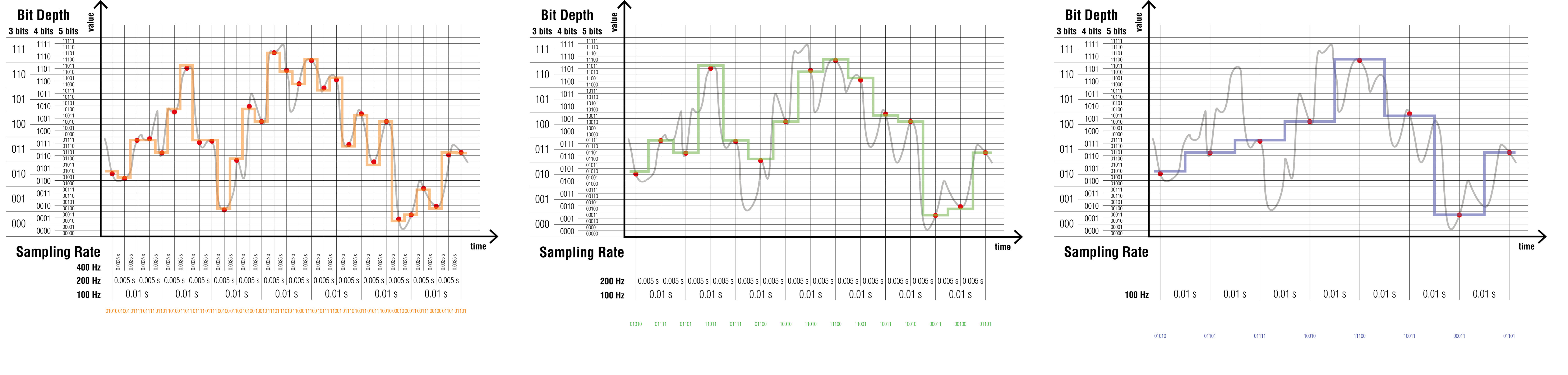
Fig. 5.5 Effet de la fréquence d’échantillonnage (sampling rate : 400, 200 et 100 Hz) sur la représentation obtenue par numérisation à une profondeur donnée (sampling depth : 5 bits). Une importante profondeur d’échantillonnage ne compense pas une fréquence d’échantillonnage insuffisante.¶
Les dispositifs électroniques dont la fonction est l’échantillonnage et la quantification des signaux sont appelés des convertisseurs analogique-numérique (CAN) ou analog to digital converter (ADC), en anglais.
5.4. Encodage¶
L’encodage de l’information numérisée se fait dans des formats de fichiers spécifiques aux applications.
Dans l’absolu, on pourrait imaginer un format universel de stockage de 0 et de 1. En connaissant la profondeur de l’échantillonnage, il serait aisément possible de reconstruire un signal. Toutefois, cela pose plusieurs problèmes.
Cela ne donnerait aucune indication sur l’interprétation qu’il faut faire de ce signal (est-ce un son ? une image ? la variation de la vitesse du vent ?) ou même les bornes de ce signal (entre 0 et \(2^n - 1\) ? entre \(-2^{(n-1)}\) et \(2^{(n-1)} - 1\) ?).
De plus, la quantité de mémoire nécessaire pour stocker et pour manipuler les données serait maximisée. Or, il est possible de construire des formats de fichiers qui exploitent les propriétés spécifiques au signal numérisé pour simplifier dans un deuxième temps le résultat de la numérisation avant de l’enregistrer. Cela débouche sur des fichiers qui sacrifient une partie de la qualité du signal numérisé en échange d’un gain sur la taille des fichiers générés. L’usage de la mémoire est ainsi économisé, mais, en contre-partie, un plus grand nombre de calculs est nécessaire pour manipuler les signaux.
C’est ainsi que des fichiers optimisés différents sont disponibles pour stocker des fichiers d’images (JPG), de vidéo (MP4), de son (MP3), ou de toute autre application. La plupart recourent pour cela à des compressions destructives au-cours desquelles une partie de l’information est abandonnée car, dans le contexte particulier, elles ne sont pas jugées indispensables.
Par exemple, la reproduction exacte des nuances de bleu du ciel importe peu pour un film d’action. Pourtant, ces mêmes nuances sont essentielles pour la reproduction d’un tableau de Monnet…
5.5. Reconstruction¶
On appelle reconstruction le processus qui transforme un signal numérisé en une variation continue d’une grandeur physique.
Les dispositifs électroniques dont la fonction est la reconstruction des signaux sont appelés des convertisseurs numérique-analogique (CNA) ou digital to analog converter (DAC), en anglais. La sortie du convertisseur est généralement une tension électrique proportionnelle à l’intensité du signal.