4. Algorithmes de tri [niveau avancé]¶

Nous venons de voir que pour rechercher de manière efficace, les données doivent être triées. Mais quelle est la complexité de l’algorithme du Tri par sélection vu dans le chapitre Trie, cherche et trouve ? C’est sa complexité qui nous donnera une indication sur sa rapidité.

4.1. Tri par sélection¶

Pour rappel, l’algorithme du Tri par sélection parcourt le tableau à la recherche des plus petits éléments. Afin de trouver le plus petit élément du tableau, il faut commencer par parcourir tous les éléments du tableau. Cette opération prend \(cn\) instructions : \(c\) instructions pour l’accès et la comparaison des éléments du tableau, multiplié par le nombre d’éléments \(n\). Il faut ensuite trouver le plus petit élément des éléments restants \(n-1\), et ainsi de suite. Concrètement, on va parcourir jusqu’à \(n\) éléments, \(n\) fois (pour chacun des éléments). La complexité du Tri par sélection est donc proportionnelle à \(n * n\) (\(n^{2}\)), on parle de complexité quadratique.

Pour aller plus loin – Calcul de complexité

Si vous souhaitez connaître les détails du calcul de complexité, cliquez pour lire ce qui suit.

Pour calculer la somme totale d’instructions nécessaires, il faut additionner les termes qui permettent de retrouver le plus petit élément. La première fois que l’on recherche le plus petit élément il faut parcourir \(n\) éléments. La deuxième fois, il reste à parcourir \(n-1\) éléments. La troisième fois, il faut parcourir les \(n-2\) éléments restants. Et ainsi de suite, jusqu’à ce qu’il ne reste plus qu’un élément.

Par exemple, si le tableau contient les éléments [5, 2, 3, 6, 1, 4], pour trouver le plus petit élément \(1\) à la première itération on doit parcourir tout le tableau, ou \(6\) éléments. A la deuxième itération, on met l’élément \(1\) de côté et on parcourt le tableau [5, 2, 3, 6, 4], ce qui fait \(5\) éléments. On met le plus petit élément \(2\) de côté et dans la troisième itération on parcourt le tableau [5, 3, 4, 6], ce qui fait \(4\) éléments. On met \(3\) de côté et on parcourt encore le tableau [5, 4, 6], ce qui fait \(3\) éléments. Finalement on se retrouve avec les tableaux [5, 6] à \(2\) éléments et [5] à \(1\) élément. La somme totale d’éléments parcourus est \(6 + 5 + 4 + 3 + 2 + 1 = 21\).

Si on généralise on obtient :

\(n + (n-1) + (n-2) + ... + (n/2 + 1) + n/2 + ... + 3 + 2 + 1\)

En réarrangeant les termes deux par deux de l’extérieur vers l’intérieur on obtient plusieurs fois le même terme :

\((n + 1) + ((n-1) + 2) + ((n-2) + 3) + .... + ((n/2 + 1) + n/2)\)

\((n + 1) + (n + 1) + (n + 1) + .... + (n + 1) =\)

\((n + 1) * n/2 =\)

\(n * n/2 + n/2 =\)

\(n^{2}/2 + n/2\)

Si on reprend l’exemple ci‑dessus, on aurait :

\(6 + 5 + 4 + 3 + 2 + 1 =\)

\((6 + 1) + (5 + 2) (4 + 3) =\)

\(7 *(6/2) = 7 * 3 = 21\) ou

\(6^{2}/2 + 6/2 = 36/2 + 3 = 18 + 3 = 21\)

Le terme dominant dans la somme \(n^{2}/2 + n/2\) est \(n^{2}/2\), plus n grandit plus \(n/2\) est insignifiant par rapport à \(n^{2}/2\). Par exemple, pour \(n = 1000\), \(n^{2}/2\) vaut \(500000\), alors que \(n/2\) vaut seulement \(500\).

Cette somme nous donne le nombre d’éléments parcourus. Mais pour chacun de ces éléments, plusieurs instructions sont exécutées, comme l’accès aux éléments et leur comparaison. Ces instructions et le terme qui divise par \(2\) peuvent être absorbés dans une constante \(c\) qui multiplie le terme quadratique \(n^{2}\). En ajoutant une constante a pour prendre en compte le nombre d’instructions qui ne dépendent pas de la taille des données (comme les initialisations au début de l’algorithme), on obtient l’ordre de grandeur \(cn^{2} + a\). L’ordre de grandeur est donc quadratique.

Si on compare les complexités vues jusqu’ici pour un tableau de \(1000\) éléments on obtient :

Complexité	Instructions élémentaires pour 1000 éléments
Linéaire	1000
Logarithmique	10
Quadratique	1000000

Avec une complexité quadratique, le Tri par sélection est un algorithme relativement lent.

Exercice 1 – Complexité du Tri par insertion

Quelle est la complexité de l’algorithme de Tri par insertion ? En d’autres termes, si le tableau contient n éléments, combien faut‑il d’instructions pour trier ce tableau ? Pour rappel, le Tri par insertion parcourt le tableau dans l’ordre et pour chaque nouvel élément, l’insère à l’emplacement correct des éléments déjà parcourus.

Solution 1 – Complexité du Tri par insertion

Exercice 2 – Complexité du Tri à bulles

Quelle est la complexité de l’algorithme de Tri à bulles ? En d’autres termes, si le tableau contient n éléments, combien faut‑il d’instructions pour trier ce tableau ? Pour rappel, le Tri à bulles compare les éléments deux par deux en les réarrangeant dans le bon ordre, afin que l’élément le plus grand remonte vers la fin du tableau tel une bulle d’air dans de l’eau. Cette opération est répétée n fois, pour chaque élément du tableau.

Solution 2 – Complexité du Tri à bulles

4.2. Tri rapide¶

Les trois algorithmes de tri vus dans le chapitre précédent – le Tri par sélection, le Tri par insertion et le Tri à bulles – sont des algorithmes de complexité quadratique. Si on devait utiliser ces tris dans les systèmes numériques en place, on passerait beaucoup de notre temps à attendre. Il existe d’autres algorithmes de tri qui sont bien plus rapides. Nous allons voir un algorithme de tri tellement rapide, qu’on lui a donné le nom Tri rapide.

On commence par prendre un élément du tableau que l’on définit comme élément pivot. Cet élément pivot est en général soit le premier ou le dernier élément du tableau, soit l’élément du milieu du tableau ou encore un élément pris au hasard. On compare ensuite tous les autres éléments du tableau à cet élément pivot. Tous les éléments qui sont plus petits que le pivot seront mis à sa gauche et tous les éléments qui sont plus grands que le pivot seront mis à sa droite, tout en conservant leur ordre (voir la deuxième ligne de la figure ci‑dessous).

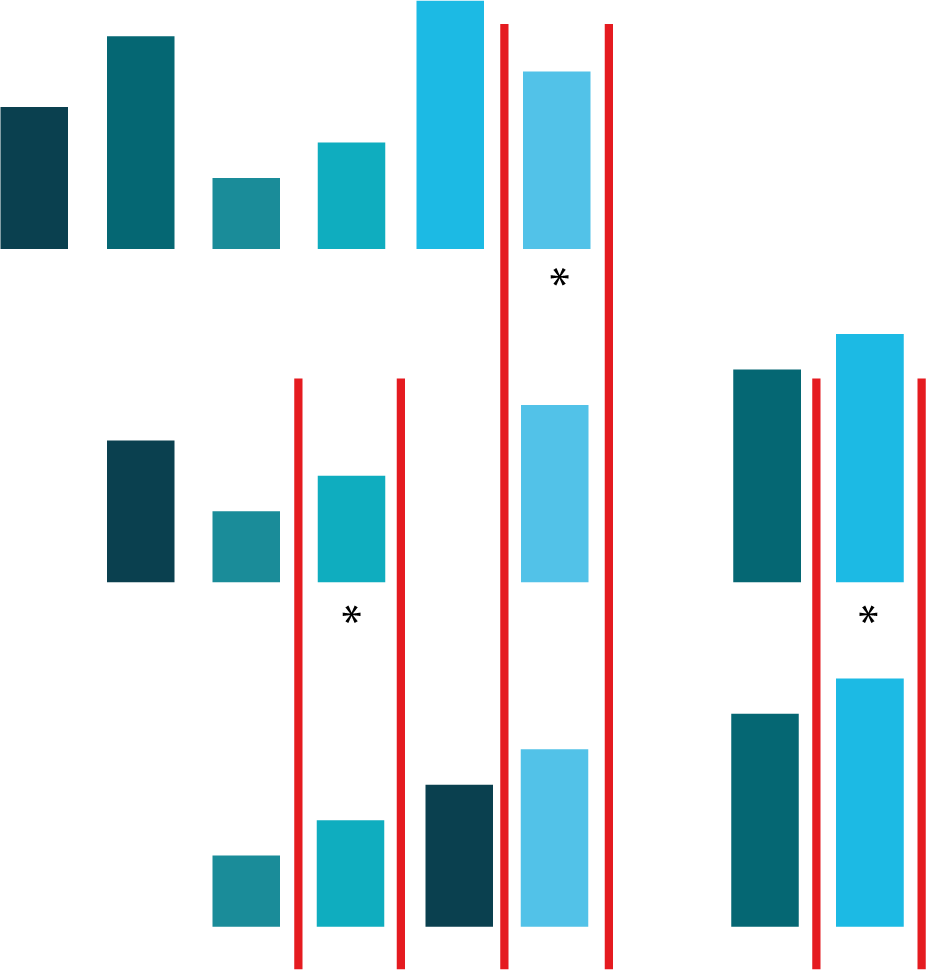
tri rapide — Fig. 4.9 **Tri rapide**. Illustration du tri rapide sur les mêmes données que celles utilisées pour illustrer les algorithmes de tri du chapitre précédent. On choisit comme élément pivot le dernier élément des tableaux à trier. Tous les éléments qui sont plus petits que le pivot se retrouvent à sa gauche, tous les éléments plus grands que le pivot se retrouvent à sa droite. L’ordre est conservé.¶

Après la répartition des éléments autour de l’élément pivot en fonction de leur taille, on se retrouve avec deux tableaux non triés, un sous‑tableau à chaque côté de l’élément pivot. On répète les mêmes opérations que pour le tableau initial. Pour chaque sous‑tableau, celui de gauche et celui de droite du pivot, on détermine un nouvel élément pivot (le dernier élément du sous‑tableau). Pour chaque nouvel élément pivot, on met à gauche les éléments du sous‑tableau qui sont plus petits que le pivot et on met à droite les éléments du sous‑tableau qui sont plus grands que le pivot. On répète ces mêmes opérations jusqu’à ce qu’il ne reste plus que des tableaux à \(1\) élément (plus que des pivots). A ce stade, le tableau est trié.

Intéressons‑nous maintenant à la complexité de cet algorithme. A chaque étape (à chaque ligne de la figure ci‑dessus), on compare tout au plus \(n\) éléments avec les éléments pivots, ce qui nous fait un multiple de \(n\) instructions élémentaires. Mais combien d’étapes faut‑il pour que l’algorithme se termine ?

Dans le meilleur cas, à chaque étape de l’algorithme, l’espace de recherche est divisé par \(2\). Nous avons vu dans le chapitre Recherche binaire que lorsqu’on divise l’espace de recherche par deux, on obtient une complexité logarithmique. Le nombre d’étapes nécessaires est donc un multiple de \(log(n)\).

Pour obtenir le nombre total d’instructions élémentaires on multiplie le nombre d’instructions par étape avec le nombre d’étapes. La complexité que l’obtient est une fonction de \(nlog(n)\), il s’agit d’une complexité linéarithmique. Un algorithme avec une complexité linéarithmique est plus lent qu’un algorithme de complexité linéaire (la recherche linéaire) ou de complexité logarithmique (la recherche binaire). Par contre, il est bien plus rapide qu’un algorithme de complexité quadratique (le tri par sélection). La figure ci‑dessous permet de comparer la vitesse de croissance des complexités étudiées jusqu’ici. Le tri rapide est donc vraiment l’algorithme de tri le plus rapide vu jusqu’ici et la complexité nous permet de comprendre pourquoi c’est le cas.

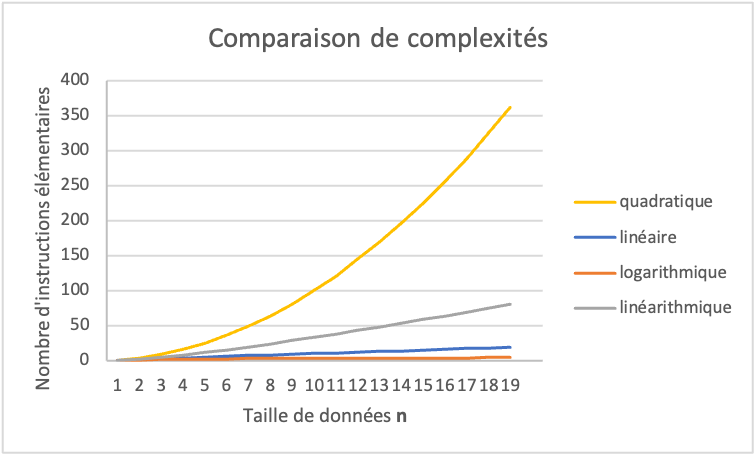
comparaison des complexités vues jusqu'ici — Fig. 4.10 **Comparaison de complexités**. La vitesse de croissance en fonction de la taille du tableau n est montrée pour toutes les complexités vues jusqu’ici. Plus le nombre d’instructions élémentaires est grand en fonction de la taille des données, plus l’algorithme est lent.¶

La première question que l’on se pose lorsqu’on analyse un algorithme est son ordre de complexité temporelle. Si l’algorithme est trop lent, il ne sera pas utilisable dans la vie réelle. Pour le problème du Tri, la stratégie « diviser pour régner » vient à nouveau à la rescousse.

Exercice 3 – Le pire du Tri rapide

Que se passe-t-il si on essaie de trier un tableau déjà trié avec l’algorithme du Tri rapide, en prenant toujours comme pivot le dernier élément ? Essayer par exemple avec le tableau [1, 2, 3, 4, 5, 6, 7].

Combien d’étapes sont nécessaires pour que l’algorithme se termine ? Quelle est la complexité dans ce cas ? Est‑ce qu’un autre choix de pivot aurait été plus judicieux ?

Solution 3 – Le pire du Tri rapide

Pour aller plus loin

Même si deux algorithmes de tri ont la même complexité temporelle, c’est‑à‑dire qu’ils prennent un temps comparable pour trier des données, ils ne prennent pas la même place en mémoire. Pour un algorithme qui prend peu de place en memoire (par exemple le tri par insertion), on dit qu’il a une plus petite « complexité spatiale ».

Si on trie un tableau qui est en fait déjà trié avec le tri par insertion, la complexité dans ce cas est linéaire. Au contraire, si on trie ce même tableau avec le tri rapide, la complexité dans ce cas est quadratique. On voit donc que selon le tableau que l’on trie, le tri rapide peut être bien plus lent que le tri par insertion.

Une analyse complète d’un algorithme consiste à calculer la complexité non seulement dans le cas moyen, mais aussi dans le meilleur cas et dans le pire cas.

Pour aller plus loin

Une analyse complète va également calculer les constantes qui influencent l’ordre de complexité. Ces constantes ne sont pas importantes lors d’une première analyse d’un algorithme. En effet, les constantes n’ont que peu d’effet pour une grande taille des données \(n\), c’est uniquement le terme qui grandit le plus rapidement en fonction de \(n\) qui compte, et qui figure dans un premier temps dans l’ordre de complexité. Par contre, lorsque l’on souhaite comparer deux algorithmes de même complexité, il faut estimer les constantes et choisir l’algorithme avec une constante plus petite.

La notation « Grand O », que l’on utilise pour écrire mathématiquement la complexité, désigne en fait la complexité dans le pire cas. Les différentes complexités vues jusqu’ici seraient notées : \(O(n)\), \(O(log(n))\), \(O(n^{2})\) et \(O(nlog(n))\). Arrivez‑vous à trouver les adjectifs correspondants ?

Exercice 4 – Le meilleur et le pire du Tri par insertion

Que se passe-t-il si on essaie de trier un tableau déjà trié avec l’algorithme du Tri par insertion ? Essayer par exemple avec le tableau [1, 2, 3, 4, 5, 6, 7].

Combien d’étapes sont nécessaires pour que l’algorithme se termine ? Quelle est la complexité dans ce cas ?

Que se passe-t-il si on essaie de trier un tableau déjà trié, mais dans l’ordre inverse de celui qui est souhaité, avec l’algorithme du Tri par insertion ? Essayer par exemple avec le tableau [4, 3, 2, 1].

Solution 4 – Le meilleur et le pire du Tri par insertion

4.3. Exercices¶

Exercice 5 – Une question à un million

Si une instruction prend \(10^{-6}\) secondes, combien de temps faut‑il pour trier un tableau d’un million d’éléments avec le tri à sélection comparé au tri rapide (sans tenir compte de la constante) ?

Exercice 6 – Une question de pivot

Trier le tableau suivant avec l’algorithme de tri rapide : [3, 6, 8, 7, 1, 9, 4, 2, 5] à la main, en prenant le dernier élément comme pivot. Représenter l’état du tableau lors de toutes les étapes intermédiaires.

Est‑ce que le choix du pivot est important ?

Exercice 7 – Une question de sélection

Trier le tableau suivant avec l’algorithme de tri par sélection : [3, 6, 8, 7, 1, 9, 4, 2, 5] à la main. Représenter l’état du tableau lors de toutes les étapes intermédiaires.

Exercice 8 – Une question d’insertion

Trier le tableau suivant avec l’algorithme de tri par insertion : [3, 6, 8, 7, 1, 9, 4, 2, 5] à la main. Représenter l’état du tableau lors de toutes les étapes intermédiaires.

Exercice 9 – Une question de bulles

Trier le tableau suivant avec l’algorithme de tri à bulles : [3, 6, 8, 7, 1, 9, 4, 2, 5] à la main. Représenter l’état du tableau lors de toutes les étapes intermédiaires.

Exercice 10 – Une question de chronomètre 🔌

Créer une liste qui contient les valeurs de \(1\) à \(n\) dans un ordre aléatoire, où \(n\) prend la valeur \(100\). Implémenter au moins deux des trois algorithmes de tri vu au cours.

A l’aide du module time et de sa fonction time(), chronométrer le temps prend le tri d’une liste de \(100\), \(500\), \(1000\), \(10000\), \(20000\), \(30000\), \(40000\) puis \(50000\) nombres. Noter les temps obtenus et les afficher sous forme de courbe dans un tableur.

Ce graphique permet de visualiser le temps d’exécution du tri en fonction de la taille de la liste. Que peut‑on constater ? Sur la base de ces mesures, peut‑on estimer le temps que prendrait le tri de 100000 éléments ? Lancer votre programme avec 100000 éléments et comparer le temps obtenu avec votre estimation.

Ai-je compris ?

Vérifiez votre compréhension :

Je sais que grâce à la stratégie algorithmique « diviser pour régner », je ne passe pas mon temps à attendre que l’ordinateur me donne une réponse.
Je sais comment trier de manière rapide.
Je sais que la complexité temporelle peut changer selon la configuration des données, en plus du cas moyen, il est également utile d’estimer le pire et le meilleur cas.